Pia Hansen has a message for teachers and parents: math has changed.
Or, to be more specific, math teaching has changed. The new methods, she told a room full of math teachers in Indianapolis last month, are good for helping more kids understand how math works.
But sometimes it’s up to students and teachers to help parents get it, too.
Hansen’s session on teaching kids the building blocks for solving math problems at the national conference National Council of Teachers of Mathematics in late October at the Indianapolis Convention Center drew a crowded room of teachers who came to learn techniques to communicate math concepts visually with hand-held “number racks,” by having kids draw pictures to explain their answers and simply by using more precise language.
In Indiana, where new academic standards now call for students to demonstrate better mastery of math through a deeper understanding of the reasons that lead them to choose a particularly strategy to solve a problem, the ideas are especially useful.
The new standards, which detail what children must know, call for students to not just learn facts, but understand how to get answers. They learn the intuition behind borrowing in subtraction problems or figure out why an author made certain choices when writing a book. This higher level thinking and analysis helps kids be better prepared to go to college or the workforce, educators say.
Hansen, a former math teacher now with Oregon nonprofit The Math Learning Center, said it’s about time math was taught more like English, where memorization takes a back seat to understanding meaning.
“It’s not rote memorization,” Hansen said. “It’s all about thinking strategies.”
New strategies seek higher-level thinking
For some of her parents, who may have learned their basic math a generation ago, Natalie Merz’s second-grade math lesson might look pretty unfamiliar.
The long worksheets of stacked numbers to add, subtract, multiply or divide are gone. Students in her class at Indianapolis Public School 61 work on fewer problems at a time, working to explain how they came to their answers.
And although a math worksheet even five years ago would probably have a strict time limit — how many can you answer in one minute? — this activity had no such pressure.
But giving fewer problems and more time lets students work at their own paces and allows them develop better problem-solving skills. Rushing through timed tests, Hansen said, makes it harder for a struggling student to discover problem-solving strategies that work best for them. That can mean they actually learn less math and feel more frustration with the subject.
As she moved from group to group, Merz made gentle suggestions to her students who weren’t going far enough to explain why.
“Don’t try to do it in your head,” she told one group. “Draw a picture.”
Some students still counted on their fingers or borrowed to solve a subtraction problem and then went back to illustrate it. But most of them followed the directions: they drew a picture and wrote down the answer.
A correct “picture” next to the equation looked something like this, with tally marks visually representing numbers in the “tens” place and circles representing those in the “ones” place.
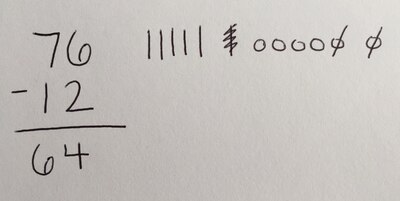
Merz was reinforcing the concept that students must recognize which numbers are “tens” and which are “ones” to fully grasp the concept of place value in addition and subtraction.
In schools strained by poverty, where children come from families with limited resources, students often struggle to articulate how they got an answer, teachers said. Teachers have to work to bridge the gap with wealthier students, where extra reading, study or academic conversation at home can help prepare kids to better explain what they mean, because the benefit of understanding how they solved a problem doesn’t just end in second grade.
“My fiance does computer programming, and he has to understand the ‘why’ logic behind what he does works,” Merz said. “There’s a process behind those jobs. I think a lot of other countries have been doing that reasoning-based math a lot more. Especially with math, it builds so much. If you don’t understand math addition, you don’t get multiplication, division, algebra or calculus.”
But when kids learn math a new way, it can make it harder for their parents not just to help them with schoolwork, but to even follow the logic themselves.
An emerging parent-child divide
At the conference, Hansen told a true story that illustrated this problem.
A father and daughter she knows were working together on the problem 17 times 99, she said. The father believed his approach was best — multiplying 17 by 99 on paper the way he learned to do it:
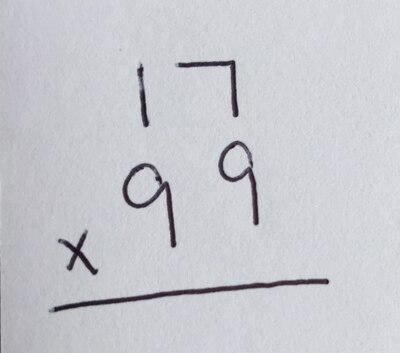
The daughter tried to solve it differently using a strategy called “grouping.” Her approach would break numbers down and re-group them in ways that can make the problem easy to solve quickly.
The daughter thought it was easier to multiply 100 times 17. Then, she told her dad, she would solve that equation by taking away one “group” to get the answer to the original problem.
“A group of 99?” he asked, puzzled.
“No,” she said in a matter-of-fact tone, “A group of 17.”
She calculated 17 times 100 to be 1,700 and then subtracted one group of 17 to find the correct answer: 1,683.
But her dad needed more explanation. So she drew him a picture.
The daughter illustrated her answer by drawing a grid with 17 rows and 100 columns. Altogether, the grid had 1,700 squares. When she subtracted one row of 17 squares, or taking away one group of 17 as she had said before, what was left was 1,683 boxes.
“Yeah,” he told his daughter. “I get it now.”
Visuals, Hansen said, such as number lines or grids, can help students to more quickly develop comfort with numbers and lead them to understand why a problem-solving process was used in the first place. The daughter not only knew how to get the answer, but she clearly understood the concepts behind multiplication — well enough to teach them to her father.
“Give them strategies,” Hansen told the teachers, “then drill facts.”
A different way of thinking about numbers
IPS’ curriculum team has both the new standards, and the new thinking about math, in mind when it advocates for the new strategies.
Curriculum coaches Nick Meyer and Eric Beebe believe if students learn to work through math strategies without help, it won’t just benefit them in school and in college but also better prepare them to consider the high tech jobs of the future.
“Understanding the relevance increases student engagement, but it also helps students be more successful because they can make connections from math to the everyday world,” Beebe said. “It also kind of opens the doors for them to understand what careers are associated with math and how math drives so much of what happens around us.”
But to get to there, kids have to master the basics that many adults take for granted.
Some teachers call the adult approach of doing math inside the head “mental math.” But relying on such a strategy without knowing the reasoning behind it can slow a child’s progress toward understanding.
Consider the problem 9 + 7, Hansen said. This is a problem the entire room of teachers could all do in their heads.
But when Hansen asked teachers to explain their answers, they gave a variety of different methods, but all used the same concept: grouping.
One volunteer wanted to make 9 into a 10 to make adding easier. So she split seven in two parts — a one and a six — then took the one and added it to nine. Now she had 10 and six, which add easily to make 16.
Another volunteer saw instinctively that borrowing could work the other way. She split nine in two parts — making an eight and one — then took the one to add with seven. Now she had eight plus eight, which she thought was easier to calculate to the same right answer: 16.
Hansen drew out the solutions and projected them on a screen. They looked something like this, with the arrows indicating how the broken down numbers were combined with the other to get the answer:
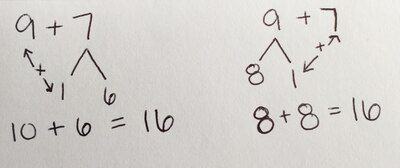
This strategy, at its core, shows the kind of thinking higher-level math the new standards encourage students to employ. Many adults use them instinctively. But young children must be taught how to understand numbers that way, or they are likely to resort to counting by ones or memorizing, Hansen said.
“I don’t want you to promote one-by-one counting,” Hansen told the teachers. “I want (students) to think in chunks and groups . . . (visuals) that support that one-by-one counting are the death of us.”
If the methods to solve the new problems seem complicated, it’s because they are, she said. The goal is to help kids reach a higher standard of academic reasoning. The standard algorithm — numbers stacked on top of each other with a plus or minus sign — can lead to the right answer. But it doesn’t get at the understanding behind the math — it takes more effort and thinking for students to explain why that was the best way to solve the problem.
“We could do the algorithm we learned,” Hansen said. “But we wouldn’t be able to justify. Now, standards ask students to justify that.”


